I’ve always had a problem with the pervasive assumption in transportation research that everyone takes the shortest metric distance path when travelling between A and B. This idea doesn’t seem to have any solid foundations in research, and intuitively it doesn’t make much sense – how do you even know what the shortest distance path is anyway?
So a good deal of my research has looked into what people really do. I’m not going to reveal all here – journal papers are generally more important than blogs in assuring future employment – but I’ll share one interesting finding.
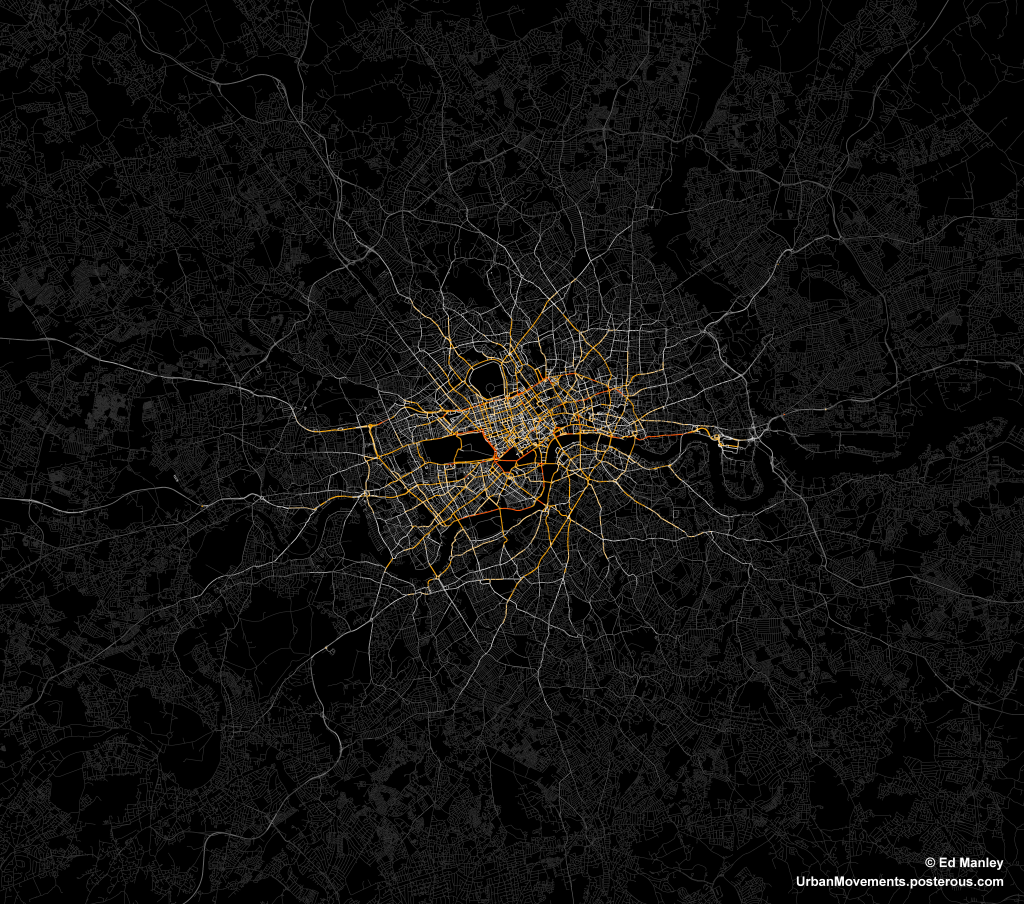
The data I have used relates to 700,000 taxi routes through London (you might remember I blogged about this dataset previously). For each of these routes, between origin and destination, I have also calculated an optimum path, according to a range of metrics, one being distance. Then, as far as this blog post goes, I have compared each route and calculated the percentage match between the real route and the optimum shortest distance journey.
Realistic?
So is the shortest distance path a decent representation of reality? No.
On average, the shortest distance path is able to estimate only 39.8% of each route. Pretty poor when you consider that it is often used solely in predicting the behaviour of many individuals.
Not only this, the data shows that the shortest distance path is followed in entirety only very rare occasions. Only 5% of real journeys show a match with 90% of their equivalent shortest distance path, with this value only rising to 13% when that threshold is dropped to 75%.
Minimising Distance
So, do people have no consideration for distance when they route through the city? Well, no, that isn’t quite the case.
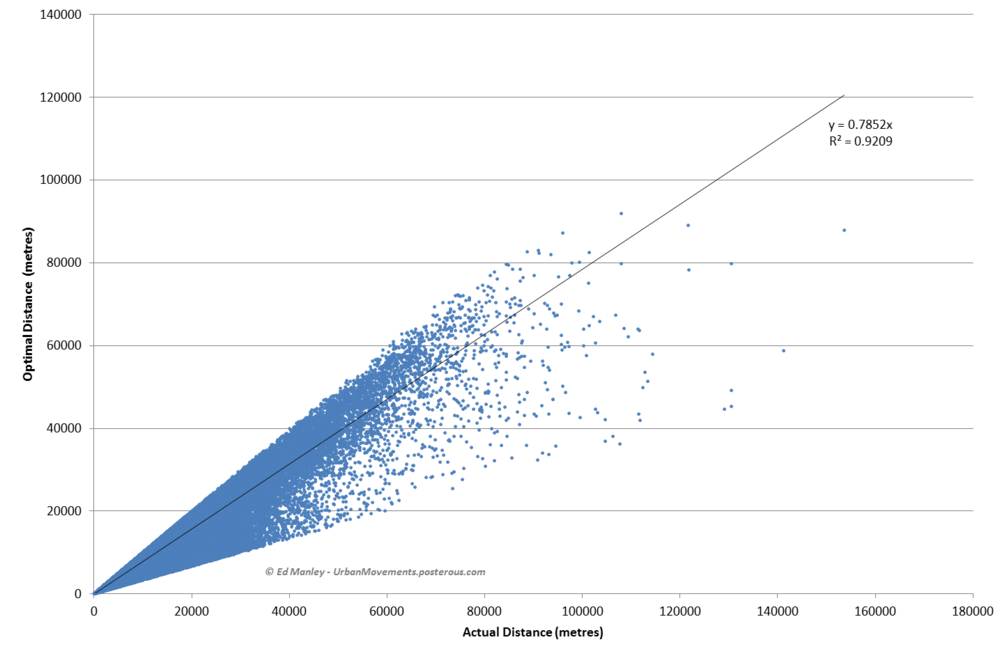
The graph below shows a scatter plot of real distances against actual distances. As you can see, the relationship and resulting R-square is pretty good.
Note: Overly long routes (three times optimal distance) have been removed.
It appears that people therefore appear to minimise distance – or they at least do not at least go extremely far from the minimal – but do not generally take the optimal shortest distance path.
This is research I’m still pulling together, but I hope this post has interest to the wider community. For anyone that is interested, do get in touch and I’ll let you know when the paper on this may be out.